백준 2609번: 최대공약수와 최소공배수

백준 2609번: 최대공약수와 최소공배수

 

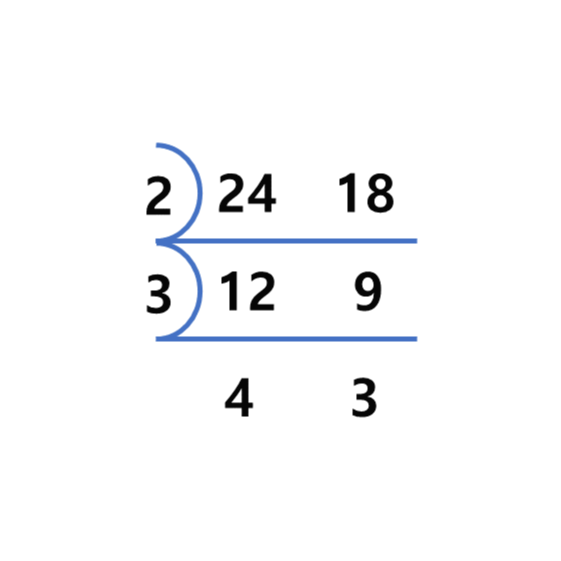
- 최대공약수와 최소공배수를 구하는 가장 널리 알려진 방법입니다. 이러한 방법을 for문을 이용하여 코드를 만들면 아래와 비슷한 코드를 만드실 수 있을 겁니다. 하지만 시간 초과에 걸려 통과하지 못합니다.

 

- 이 문제는 "유클리드 호제법"을 사용하여 풀어야 합니다.

유클리드 호제법이란,

두 양의 정수 a, b (a > b)에 대하여 a = bq + r (0 ≤ r < a)라 하면, a, b의 최대공약수는 b, r의 최대공약수와 같다.

- 아래 gcd(greatest common divisor) 매소드는 유클리드 호제법을 알고리즘으로 나타낸 것입니다.

  24와 18을 예로 들면,

1.  a = 24, b = 18, tmp = 6   -> a = 18, b = 6
2. a = 18, b = 6, tmp = 0 -> a = 6, b = 0
3. return a = 6

-최소공배수는 최대공약수를 활용하여 쉽게 구할 수 있습니다.

https://terms.naver.com/entry.nhn?docId=3338367&cid=47324&categoryId=47324

- 위 사진을 참고하여 매소드를 만들면 아래의 lcm(least common multiple) 매소드가 됩니다.